From my experience, getting used to traversing non-linear data structures takes a bit of time. So when you try to get hold of trees, you need something easy to practice and finding maximum depth of binary tree is a great place to start.

The problem can be solved both iteratively and recursively but the iterative approach can produce not-so-easy-to-understand code. Thus, I am going to share with you only the recursive solution.

So What's The Problem?

Oh, it is quite simple. Given the root of a binary tree, return its maximum depth.

This basically means finding the number of nodes along the longest path from the root node down to the farthest leaf node.

And yes, you may have seen it on LeetCode

How Do We Go About It?

Well, we simply need to count the nodes along each path - the highest count is what we are looking for.

If our binary tree would look like the one below, we would need to check two paths (5 -> 3 -> 4 and 5 -> 7). Since there are 3 nodes along the left path and 2 along the right path and we are looking for the maximum depth, 3 would be our answer.

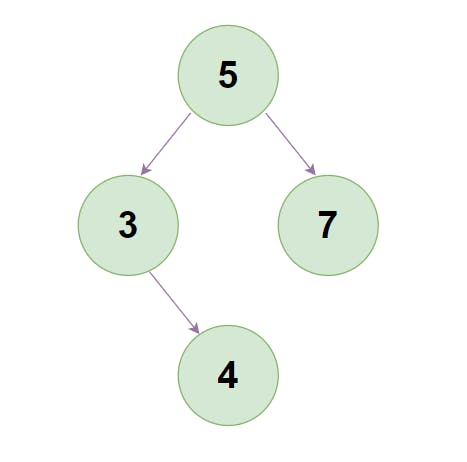
Now, let's try to think about it recursively. The left path consists of the root and a sub-tree attached to it. Similarly, the right path includes the root and its own sub-tree. Thus, to determined the length of a path, we need to find the maximum depth of each sub-tree.

Since each sub-tree may have its own root and possibly another sub-tree attached, we need to check each of those sub-trees too... We keep repeating this until the sub-tree we currently investigate is empty. This means it is time to start going back up!

How Does It Look In Practice?

The code is surprisingly simple! We start with our base case which is an empty tree. Since there are no nodes in the tree, we return 0.

Otherwise, recursively we get the maximum depth of the left and right sub-trees. Once we have them, we choose the one that is greater and we increase it by 1 to accommodate for the node we are currently processing.

In other words, we do this:

def find_max_depth(node):
  if node is None:
    return 0

  left = find_max_depth(node.left)
  right = find_max_depth(node.right)

  return max(left, right) + 1

And if you need a simple definition of binary tree node, here is one:

class Node:
  def __init__(self, val, left, right):
    self.value = val
    self.left = left
    self.right = right

What About The Time Complexity?

The time complexity of find_max_depth is determined by the two recursive calls. All other instructions can be ignored because they are O(1). So to get the complexity of our solution, we need to check how many recursive calls are done depends on the tree size.

For example, a tree with a single node needs 3 recursive calls whereas the one with 3 nodes will execute find_max_depth 7 times. And if we increase the number of nodes to 7, then we will get 15 recursive calls.

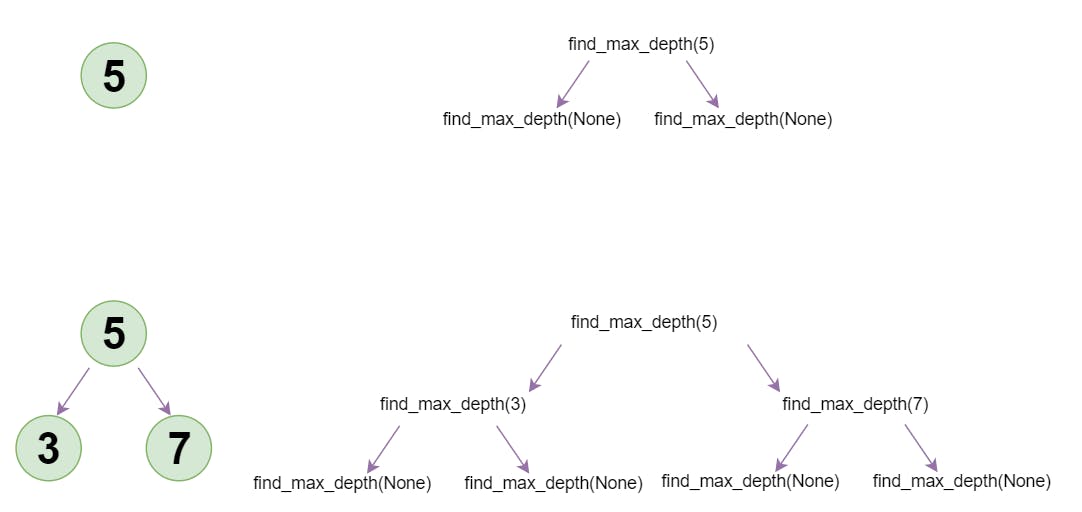
So we can see that there seems to be some kind of relation between the number of nodes and the number of recursive calls. Let's try to find it!

# n is the number of nodes in tree
n = 1 -> 3 = 2 + 1 = 2 * 1 +1 = 2n + 1
n = 3 -> 7 = 6 + 1 = 2 * 3 + 1 = 2n + 1  
n = 7 -> 15 = 14 + 1 = 2 * 7 + 1 = 2n + 1

It turns out that the number of recursive calls can be expressed as 2n+1 in relation to the number of nodes n. This means the time complexity is O(2n+1) but because we only care about the dominant terms, we simplify to O(n)!

---

The cover image was created with the help of all-free-download.com